在摸鱼中学习蒙特卡罗方法

引言

最近一道小学六年级的几何题在煎蛋上掀起了一波摸鱼浪潮，我一看确实是一道小学题，因为用定积分一下就算出来了，too simple。但是我小学毕业太久了，都忘记如何积分了//误。
所以趁此机会学习一下用蒙特卡罗方法(Monte Carlo Method)来解此题。

概述

蒙特卡罗方法诞生于上个世纪40年代美国的”曼哈顿计划”，名字来源于赌城蒙特卡罗，象征概率。
P.S. 还有一种随机方法叫拉斯维加斯方法，同样名自另一座赌城拉斯维加斯。

蒙特卡罗方法是一种计算方法。原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。
它非常强大和灵活，又相当简单易懂，很容易实现。对于许多问题来说，它往往是最简单的计算方法，有时甚至是唯一可行的方法。

Hello World

第一个例子我们来看看如何使用蒙特卡罗方法来估算 π 的值。

估计 π
面积公式
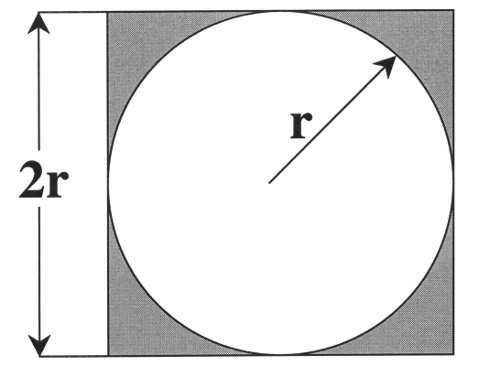
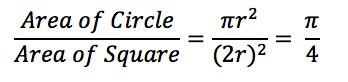
正方形内部有一个相切的圆，它们的面积之比是 π/4。

随机点
现在，在这个正方形内部，随机产生 10000 个点（即 10000 个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。

如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以 4，就是 π 的值。

下面是 Python 实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import math
import random


r = 1  # radius
n_all = 10000  # number of random samples
n_in = 0  # number of points in circle

for _ in range(n_all):
    x = random.uniform(-r, r)
    y = random.uniform(-r, r)

    # Euclidean distance, center = (0, 0)
    distance = math.sqrt(math.pow(x, 2) + math.pow(y, 2))

    if distance < r:
        n_in += 1

pi = (n_in / n_all) * 4
print(pi)

输出 3.14187

解题

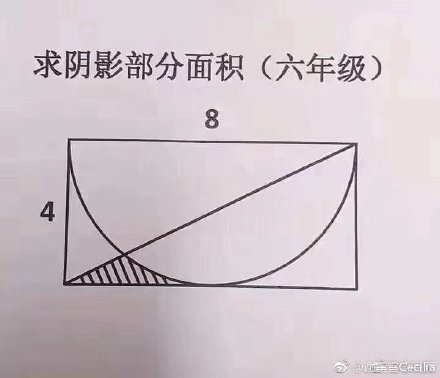
小学六年级的几何题
开始解题，不要慌，先暗中观察一番：整个图为宽 8 高 4 的矩形，阴影存在于直线下和圆外左下。

首先以左下角为原点，建立坐标系。圆心在 (4, 4)，半径 r = 4。

然后写出直线方程: y = 1/2 * x => 在直线下面则: y < 1/2 * x

再写出在圆外方程: sqrt((x - 4) ^ 2 + (y - 4) ^ 2) > r

此外阴影还需满足: x < 4

Python 实现如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import math
import random


r = 4  # radius
w = 8  # width
h = 4  # height

n_all = 10000  # number of random samples
n_in = 0  # number of points in shadow

for _ in range(n_all):
    x = random.uniform(0, w)
    y = random.uniform(0, h)

    if x < 4 and \
       y < 0.5 * x and \
       math.sqrt(math.pow(x - 4, 2) + math.pow(y - 4, 2)) > r:
       n_in += 1

area = (n_in / n_all) * (w * h)
print(area)

输出 1.2544

总结与展望

蒙特卡罗算法并不是一种算法的名称，而是对一类随机算法的特性的概括，它指的是时间复杂度固定，然而结果有一定几率失败，而采样越多，越近似最优解的算法。
此题还可以使用矩形法或梯形法来实现定积分的逼近，编程实现也非常简单//逃。

References